For classification problems, it's hard to use linear regression to predict an accurate difference between two classes as it does not indicate a strict enough differentiation between the two. We use a steeper curve with logistic regression to create a more accurate classifier.
The code to import a logistic regression model from the SKLearn library is as follows:

from sklearn.linear_model import LogisticRegression

This sequential approach works in a small series of steps:

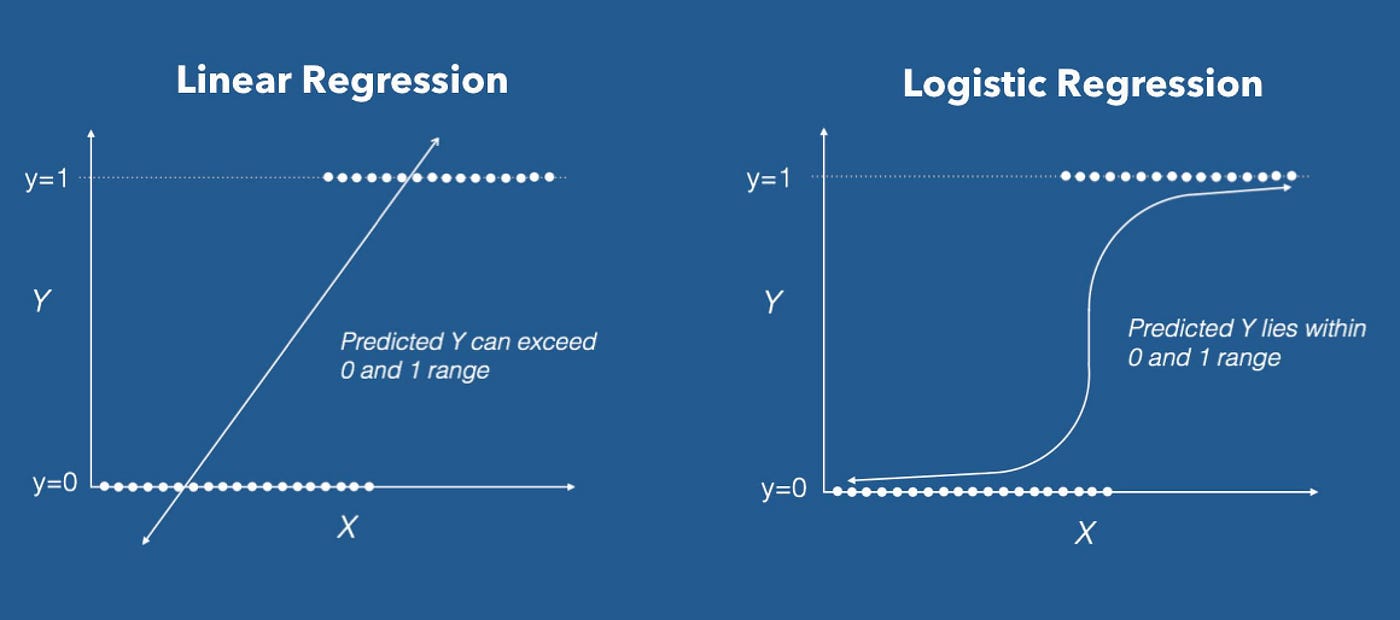
From here, predicting using Logistic Regression comes down to three elements: A predictor function, a cost function, and a threshold which acts as a hard divider between two classes. For our predictor, a Sigmoid function is used, as its characteristic S-like shape maps any real value into another value between 0 to 1. This function has a non-negative derivative at each point and exactly one inflection point, giving a clear indication of the difference between two classes (fraud or not fraud for example).

The cost function in this case would work similarly to cost functions in many other models, such as boosting ensemble methods. For Binary Logistic Regression, we use the equation to help minimize loss. As the model is trained, decreasing the cost will increase the maximum likelihood, assuming that samples are drawn from an identically independent distribution.

If you want to learn more about Logistic Regression, click the link here:

How Is Logistic Regression used as a Classification Algorithm?

Our LogReg Experience

Data and Analysis

Logistic Regression was the first model we trained as the Sigmoid approximation that it makes use of, seemed like a clear way to predict whether or not something was or wasn't fraud. It proved to be a good start, as it has a lack in abundance of hyperparameters, and was indeed a good fit for our problem, allowing this model to work with high accuracy and little fine tuning. It wasn't as accurate as some other models like RDF or Boosting, but it was still a consistent predictor.

Accuracy Score

Precision Score

Recall

ROC AUC Score